좀비처럼

Running time

알고리즘의 Running time은 알고리즘이 특정 입력을 처리하는 데 걸리는 시간을 의미하며, 알고리즘의 효율성을 평가하기 위해 사용됨

• 알고리즘의 Running time(T)에 영향을 끼치는 요소
  • input 값의 크기(n)와 정렬된 정도
  • 해당 알고리즘의 연산 수

Machine-independent time

Running time을 측정하기 위해 실제 실행 시간을 측정하는 방법을 사용할 수 있으나 사실상 사용되지 않음

왜냐하면, 한 알고리즘을 같은 장치에서 측정할 때의 Relative Speed와 다른 장치에서 측정할 때의 Absolute Speed 간의 Machine-dependent 상수가 존재하게 됨 (장치 별 하드웨어, 컴파일러 등 실행 환경 차이 존재)

따라서, Machine-dependent 상수를 무시하고 알고리즘의 실행 시간을 수학적으로 분석하는 방법을 사용

수학적 분석 방식은 알고리즘의 반복문, 조건문, 함수 호출 등을 추적하여 연산의 총 횟수를 계산함

이후 입력 크기 n값에 따른 T(n) 값의 변화를 관찰하여 함수로 나타내는 점근적 분석(Asymptotic Analysis) 방식

시간복잡도(Time complexity)

알고리즘의 실행 시간은 아래의 시간 복잡도 분류에 따라 분석함

• Worst-case (usually)
  
  • 가장 불리한 입력에서의 알고리즘의 실행 시간
  • T(n) = 크기가 n인 입력값에 대한 알고리즘의 최대 시간
• Average-case (sometimes)
  • 모든 가능한 입력에 대한 알고리즘 실행 시간의 평균값
  • T(n) = 크기가 n인 모든 입력값에 대한 알고리즘의 예상 시간
  • 입력값의 통계적 분포에 대한 가정이 필요함, 분석하기 어려움
• Best-case (bogus)
  • 가장 유리한 입력에서의 알고리즘의 실행 시간
  • 특정 입력값에서 빠르게 작동하는 느린 알고리즘을 이용한 속임수

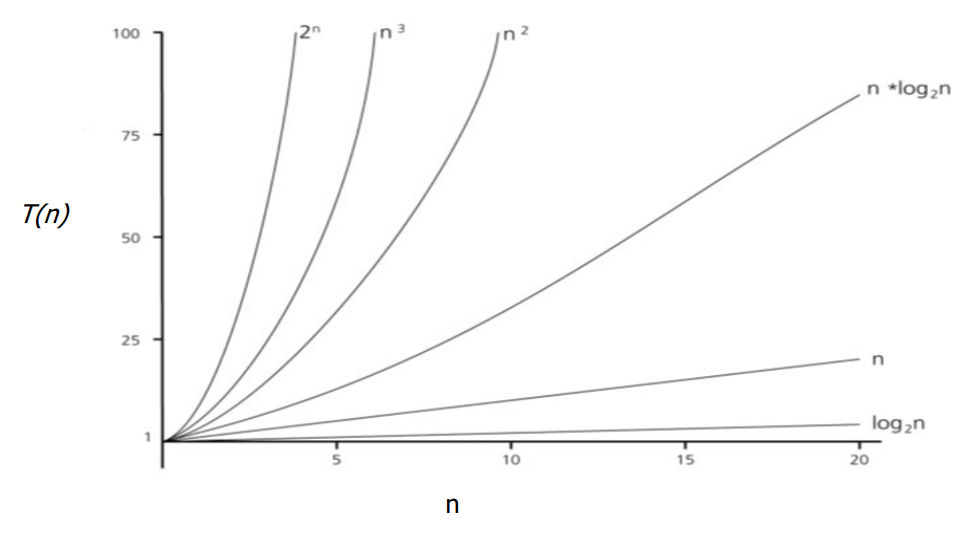
시간복잡도 표기법(notation) & Growth of Function

시간복잡도에 따른 Growth of Function(n값에 따른 함수의 추이)에 대한 Asymptotic notation을 사용

최고차항 미만의 낮은 차수의 항과 상수항은 무시하며, 로그 함수의 밑은 모두 동일하게 취급

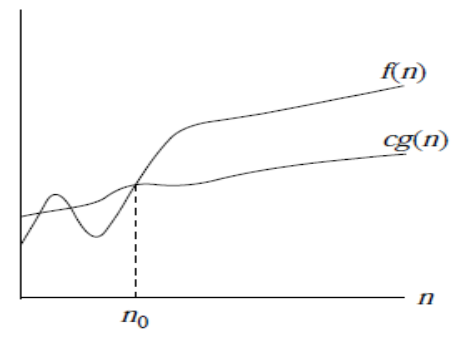
• 𝛰 - notation (Big-O notation) 
  • 𝛰(g(n)) = f(n)
  • g(n)은 f(n)의 최악의 경우에 대한 상한선 (asymptotic upper bound)
  • n ≥ n0인 모든 n에 대해 0 ≤ f(n) ≤ c g(n)인 양의 상수 c와 n0가 존재함

• Ω - notation (Big-Omega notation)
  • Ω(g(n)) = f(n)
  • g(n)은 f(n)의 최선의 경우에 대한 하한선 (asymptotic lower bound)
  • n ≥ n0인 모든 n에 대해 0 ≤ c g(n) ≤ f(n)인 양의 상수 c와 n0가 존재함

• Θ - notation (Big-Theta notation)
  • Θ(g(n)) = f(n)
  • g(n)은 f(n)의 근사치 (asymptotic tight bound)
  • n ≥ n0인 모든 n에 대해 0 ≤ c1 g(n) ≤ f(n) ≤ c2 g(n)인 양의 상수 c1, c2, n0가 존재함

+) 비주류 notation

• 𝜊 - notation (Little-o notation)
  • o(g(n)) = f(n)
  • n ≥ n0인 모든 n에 대해 0 ≤ f(n) < c g(n)인 양의 상수 c와 n0가 존재한다.
    • n^1.999 = 𝜊(n^2)
    • n^2 != 𝜊(n^2)
• 𝜔 - notation (Little-omega notation)
  • 𝜔(g(n)) = f(n)
  • n ≥ n0인 모든 n에 대해 0 ≤ c g(n) < f(n)인 양의 상수 c와 n0가 존재한다.
    • n^2.001 = 𝜔(n^2)
    • n^2 != 𝜔(n^2)

𝛰 - notation(Big-O 표기법)과 실행 시간 표현 예시

시간복잡도 표현에 주로 𝛰 - notation을 사용하며 아래는 주요 𝛰 - notation 표기법 예시임

• O(1): 상수 시간 (입력 크기 n에 관계없이 일정)
  배열의 특정 요소 접근
• O(log n): 로그 시간
  이진 탐색
• O(n): 선형 시간
  배열의 모든 요소 순회
• O(n log n): 로그-선형 시간
  효율적인 정렬 알고리즘(퀵 정렬, 병합 정렬 등)
• O(n²): 이차 시간
  중첩된 이중 루프
• O(2ⁿ): 지수 시간
  일부 재귀 기반 알고리즘(피보나치 수열)

Comparing Functions

• Transitivity (이행성)
  • f(n) = Θ(g(n))이고 g(n) = Θ(h(n))이면 f(n) = Θ(h(n)) 이다
• Reflexivity (반사성)
  • f(n) = Θ(f(n)) 이다
• Symmetry (대칭성)
  • g(n) = Θ(f(n)) 이면, f(n) = Θ(g(n)) 이다.
• Transpose Symmetry (전치 대칭성)
  • g(n) = Ω(f(n)) 이면, f(n) = O(g(n)) 이다.

알고리즘의 정의

문제 해결에 필요한 단계적 계산 절차 또는 처리 과정 순서의 집합

• 특정 작업을 수행하기 위한 유한한 명령어의 집합
• 특정 값을 입력 받고 특정 값을 출력하는 잘 정의된(Well-defined) 계산 절차
• 입력을 출력으로 변환하는 일련의 계산 단계
• 잘 명시된(Well-specified) 계산 문제를 해결하기 위한 도구

알고리즘의 조건

• 입력 (Input)
  • 외부로부터 0개 이상의 입력값이 제공되어야 함
  • 입력값은 문제를 정의하거나 계산을 시작하는 데 사용됨

• 출력 (Output)
  • 계산 절차의 결과로 적어도 하나 이상의 출력값을 생성해야 함
  • 출력값은 문제 해결의 결과물이어야 함

• 유한성 (Finiteness)
  • 모든 명령이 알고리즘 내에서 추적되는 한, 모든 경우의 결과가 반드시 유한한 수의 단계 후에 종료되어야 함
  • 무한 루프와 같이 끝없이 실행되는 과정은 알고리즘으로 인정되지 않음
• 명확성 (Definiteness)
  • 알고리즘의 각 단계는 명확하고 모호하지 않아야 하며 이중적 의미로 해석되지 않아야 함
  • 한 단계가 수행되었을 때 어떤 일이 일어나는지 명확히 정의되어야 함
• 효율성 (Effectiveness)
  • 알고리즘의 모든 단계는 실제로 수행 가능한 간략하고 기본적인 작업이어야 함
  • 이론적으로 실행할 수 없는 작업이나 무한한 자원이 요구되는 작업은 포함되지 않아야 함